確率変数(連続型や離散型)と累積分布関数・確率質量関数・確率密度関数などについて, 数学的に厳密な定式化を紹介します. 初学者向けの解説を見たい方は以下の記事を参照してください.
・確率変数・連続型と離散型【初学者向けの解説】
確率変数と累積分布関数
確率変数を厳密に定義するには, 次の関数としての見方を用いる.
確率空間 \((\Omega, \mathcal{A}, P)\) において, \(\Omega\) 上の実数値関数 \(X:\Omega \to \mathbb{R}\) で, 任意の実数 \(x\) に対して\[
\{\omega \in \Omega \mid X(\omega) \leq x\} \in \mathcal{A} \tag{1}
\]となるとき, \(X\) を確率変数という. また \(X\) の値域\[
X(\Omega)=\{X(\omega)\mid \omega \in \Omega\}
\]を \(X\) の標本空間という.
- 確率変数はr.v. (random variable) と省略することがある.
- 条件 (1) が付いているのは, 事象 \(\{\omega\mid X(\omega) \leq x\}\) に確率が定義されていることを保証するためである.
- 確率変数の標本空間は \(\mathcal{X}\) で表すことが多い.
例. コイン2枚を投げたときの表の出る枚数を \(X\) とする. このとき, 全事象は\[\Omega=\{\text{(表,表), (表,裏), (裏,表), (裏,裏)}\}, \] \(X(\cdot)\)は次のような関数(確率変数)になっている \begin{align}&X((\text{表,表}))=2,\quad X((\text{裏,裏}))=0, \\ &X((\text{表,裏}))=1, \quad X((\text{裏,表}))=1. \end{align} \(X\) の標本空間は \(
\mathcal{X}=\{0,1,2\}\) である.
標本空間という用語についての蛇足
確率変数 \(X\) の値域 \(X(\Omega)\) を「\(X\) の標本空間」というが, 全事象 \(\Omega\) のことを「標本空間」ということもある.(同じ本の中で2つのものに同じ言葉が用いられることもある.)これは, 実験や観測において起こりうる結果全体 \(\Omega\) について確率を考えていても, 実際にはそこから得られる数値 \(X(\Omega)\) だけに注目して, そこに確率を押し付けても同じことだからである.
確率変数の論理を展開をするには, 次の累積分布関数から出発するとよい.
(累積分布関数には, 連続型や離散型に限らず, どの確率分布にも定義できるというメリットがある)
確率変数 \(X\) に対して, 関数\begin{align}
&F_X(x) = P(X\leq x) \\ &=P(\{\omega \in \Omega \mid X(\omega) \leq x\})
\end{align}を累積分布関数または単に分布関数という.
確率変数 \(X\) の累積分布関数 \(F_X(x)\) は次の条件を満たす:
(F1) \(F_X(x)\) は増加関数である. つまり, \(\displaystyle a< b\) ならば \(F_X(a) \leq F_X(b)\).
(F2) \(\displaystyle\lim_{x\to -\infty} F_X(x)=0\), \(\displaystyle\lim_{x\to \infty} F_X(x)=1\).
(F3) \(F_X(x)\) は右連続関数である.
証明には確率の公理やそこから従う確率の連続性などを用いる.
詳細は → 確率の公理・確率空間・確率の連続性
証明.
(F1) \(a<b\)ならば\(\{\omega \in \Omega \mid X(w) \leq a \} \subset \{\omega \in \Omega \mid X(w) \leq b \}\). よって, 確率の単調性(\(A\subset B\, (\subset \Omega)\) ならば \(P(A) \leq P(B)\)) より
\(P(X\leq a) \leq P(X\leq b).\) したがって, \(F_X(a)\leq F_X(b)\).
(F2) \(\displaystyle\lim_{n\to \infty} x_n=-\infty\)となる任意の減少列\(\{x_n\}\) に対して, \(A_n=\{w \mid X(w) \leq x_n \}\) とおけば, \(\{ A_n\}\)は減少列であり, \(\displaystyle\lim_{n\to \infty} A_n = \emptyset\)となる. よって確率の連続性より, \begin{align}
&\lim_{n\to \infty} F(x_n) =\lim_{n\to \infty} P(X\leq x_n) \\
&=\lim_{n\to \infty} P(A_n) =P(\emptyset)=0.
\end{align} したがって, \(\displaystyle\lim_{x\to -\infty} F(x)=0\)となる.
同様に, \(\displaystyle\lim_{n\to \infty} x_n=\infty\)となる任意の数列\(\{x_n\}\) に対して, \(A_n=\{w \mid X(w) \leq x_n \}\) とおけば, \(\{ A_n\}\)は増加列であり, \(\displaystyle\lim_{n\to \infty} A_n = \Omega\) (全事象) となる. 確率の連続性より, \(\displaystyle\lim_{n\to \infty} F(x_n) %=\lim_{n\to \infty} P(X\leq x_n) %=\lim_{n\to \infty} P(A_n) =P(\Omega)=1.\) したがって, \(\displaystyle\lim_{x\to -\infty} F(x)=1\)となる.
(F3) (F2) と同様に, \(x_n\to x\) となる任意の減少列 \(\{x_n\}\) に対して, 確率の連続性より\( \displaystyle \lim_{n\to \infty} F_X(x_n) =F_X(x)\) となる. したがって \(F_X(s)\) は右連続関数である.
上の定理の逆も成り立つ. つまり, 関数 \(F(x)\) について次の同値条件が成り立つ
\(F(x)\) が (F1)~(F3) を満たす \(\Leftrightarrow\) \(F(x)\) はある確率変数の累積分布関数
(\(\Leftarrow\)) は上の定理で証明済み.
(\(\Rightarrow\)) について示す.
\(\mathcal{I}=\{(a,b] \subset \mathbb{R} \mid a\leq b\}\) を左半開区間全体の集合とする. ただし \((a,a]=\emptyset\)とみなす. \(\mathcal{I}\) の関数 \(\mu\) を \[
\mu((a,b])=F(b)-F(a), \quad \mu(\emptyset)=0
\]と定めると, (F1) から \(\mu((a,b]) \geq 0\)である. さらに \(\mu\) は集合半環 \(\mathcal{I}\) 上の前測度となる. つまり可算加法性をもつ. 実際, \(a=t_0\leq t_1 \leq t_2 \cdots \) かつ \(t_n \to b\) となる数列 \(t_n\) で \[
(a,b]=(t_0, t_1] \sqcup (t_1, t_2] \sqcup \cdots
\]と分解できるとき, \begin{align}
&\mu((a,b])=F(b)-F(a)\\
&=\sum_{n=1}^{\infty} (F(t_n)-F(t_{n-1}))=\sum_{n=1}^{\infty}\mu((t_{n-1},t_{n}])
\end{align}となる. ここで, 2つめの等式は \(F(x)\) の右連続性 (F3) から \(\lim_{n\to \infty} F(t_n)=F(b)\) が成り立つことを用いた.
したがってカラテオドリの拡張定理から, \(\mu\) は \(\mathcal{I}\) によって生成される \(\mathbb{R}\) 上の \(\sigma\)-加法族 \(\sigma(\mathcal{I})\) (\(\mathbb{R}\) におけるボレル集合族 \(\mathcal{B}(\mathbb{R})\)) に拡張できる. つまり, \(\mathcal{B}(\mathbb{R})\) 上の測度 \(\widetilde{\mu}\) で \(\widetilde{\mu} \big|_{\mathcal{I}} =\mu\) となるものが存在する. このとき \(\tilde{\mu}\) は確率測度である. つまり \(\tilde{\mu}(\mathbb{R}) =1\) を満たす. 実際, 測度の連続性と (F2) から\begin{align}
&\tilde{\mu}(\mathbb{R})=\lim_{n\to \infty} \tilde{\mu}((-n,n])\\
&=\lim_{n \to \infty} \left( F(n)-F(-n) \right)=1.
\end{align} したがって確率空間を \((\mathbb{R}, \mathcal{B}(\mathbb{R}), \tilde{\mu})\) とし, これに対する確率変数を恒等写像 \(X=id\) とすれば, \begin{align}
&\tilde{\mu} (\{x \in \mathbb{R}\mid x \leq a\})=\lim_{n\to \infty}\mu((-n, a])\\
&=\lim_{n\to \infty}(F(a)-F(-n))=F(a)
\end{align}となるため, \(F(x)\) は \(X\) の累積分布関数となる.(証明終了)
離散型確率変数
標本空間が可算集合になっているとき, その確率変数を離散型確率変数という.
確率変数 \(X\) が離散型のとき, 実数 \(\mathbb{R}\) 上の関数\[
f_X(x)=P(X=x)
\]を確率質量関数または確率関数という.
- 確率質量関数は p.m.f. (probability mass function) と省略して書くことがある.
- 離散型のとき, 累積分布関数は階段型になる.
例. 3枚のコインを投げるとき, 表の出る枚数を \(X\) とする. このとき \(X\) は離散型確率変数とみなせ, 確率量関数 \(f_X(x)\) と累積分布関数 \(F_X(x)\) は次のようになる.
\(f_X(x)=\begin{cases}
\frac{1}{8} & (x=0),\\ \frac{3}{8} & (x=1),\\ \frac{3}{8} & (x=2),\\ \frac{1}{8} & (x=3), \\0 & (otherwise)
\end{cases}\) \(F_X(x)=\begin{cases}
0 & (x< 0),\\ \frac{1}{8} & (0\leq x< 1),\\ \frac{4}{8} & (1\leq x< 2),\\ \frac{7}{8} & (2\leq x <3),\\ 1 & (3\leq x).
\end{cases}\)
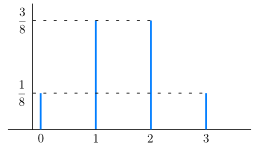
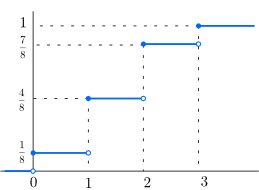
連続型確率分布
累積分布関数 \(F_X(x)\) が連続なとき, 確率変数 \(X\) は連続型であるという. また, \(F_X(x)\) が\[
F_X(x)=\int_{-\infty}^x f_X(t)dt \tag{2}
\]と積分表示できるとき, \(f_X(x)\) を確率密度関数という.
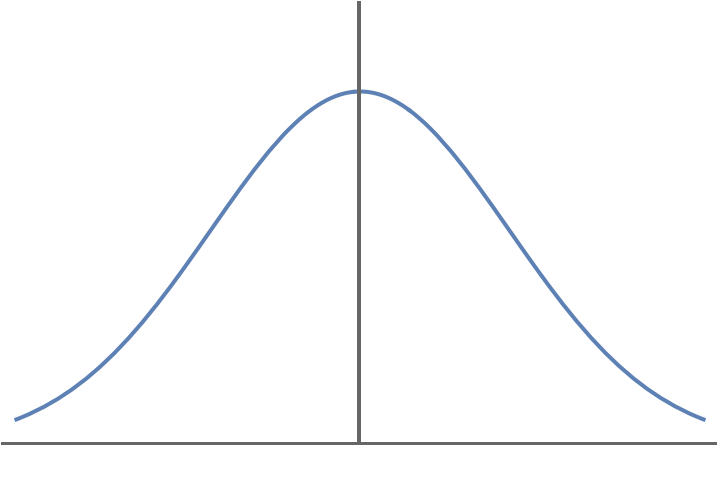
確率密度関数の例
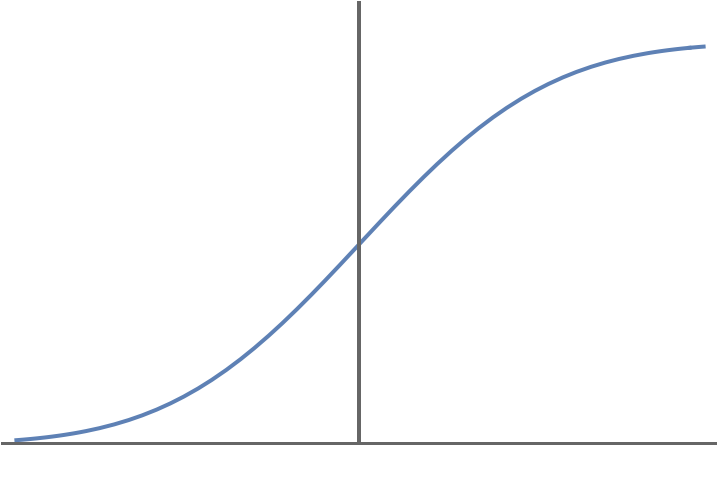
累積分布関数の例
- 確率密度関数は p.d.f. (probability density function) と省略して書くことがある.
- 確率密度関数\(f(x)\)を用いて, \[P(a\leq X \leq b)= F(b)-F(a)=\int_{a}^b f(x) dx\] と表せる.
補足. 式 (2) のような積分表示ができるときに, \(F_X(x)\) は連続型(正確には絶対連続型)ということがある. 絶対連続は連続よりも強い条件であることに注意.
確率密度関数\(f_X(x)\)は次の条件をみたす:
(D1) すべての実数 \(x\)に対して \(f_X(x)\geq 0\) .
(D2) \(\displaystyle\int_{-\infty}^{\infty} f_X(x) dx=1\).
(D3) \(f_X(x)\) の連続点において, \(F’_X(x)=f_X(x)\).
(D1)は正確には殆どいたるところ \(f(x)\geq 0\) だが, 詳細については下記の「確率密度関数の不連続点について」を参照.
証明.
(D1) 確率の非負性より従う.
(D2) 累積分布関数の性質 (F2) より従う.
(D3) 微分積分学の基本定理から成り立つ.
(D2) や (F2) は直感的には明らかだが, 真面目に示そうとすると確率の連続性を用いる必要がある. 確率の公理に, 有限加法性ではなく完全加法性が用いられているのはこのためである.
(→確率の公理・確率空間・確率の連続性)
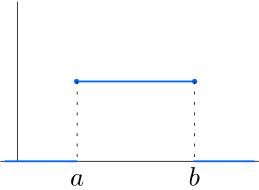
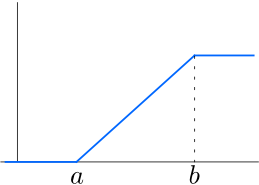
例. 次のような確率密度関数 \(f_X(x)\)(または累積分布関数 \(F_X(x)\) )をもつ分布を一様分布という.
\(f_X(x)=\begin{cases}
\frac{1}{b-a} & (a\leq x\leq b),\\
0& (x< a, \, b <x),
\end{cases}\) \(F_X(x)=\begin{cases}
0 & (x<a ),\\
\frac{1}{b-a}(x-a)& (a\leq x\leq b),\\
1 & (b<x).
\end{cases}\)
最後にいくつか, 連続型確率変数についての補足をあげておく.
確率密度関数の不連続点について
一様分布のように, 確率密度関数には不連続点が存在することがある. このような不連続点については, 確率密度関数の値をどのようにとってもよい. 例えば, 一様分布の確率密度関数は \[f_X(x)=\begin{cases}
\frac{1}{b-a} & (a\leq x\leq b),\\
0& (x< a, \, b <x),
\end{cases} \tag{3}\] ととっても, \[f_X(x)=\begin{cases}
\frac{1}{b-a} & (a< x< b),\\
0& (x\leq a, \, \leq <x),
\end{cases}\] ととってもよい. 確率・統計的に意味があるのは積分\(\displaystyle\int_{a}^b f_X(x) dx\) だけであり, このような点をどのようにとっても積分値に影響しないからである. 一般には零測度集合上の点をどのようにとっても積分値には影響しない. このことを踏まえると, 確率密度関数の性質 (D1) は正確には「殆どいたるところ \(f_X(x)\geq 0\)」と書くことになるが, 「すべての \(x\) について \(f_X(x)\geq 0\)」となる確率密度関数を代表としてとることができるため, 確率・統計の教科書ではこのことについて, わざわざ断らず, (D1)のような書き方をすることが多い. また, 確率密度関数には零測度集合上の値の分だけ任意性があるが, わざわざそれを断らずに, 例えば「 一様分布の確率密度関数は (3) である 」などと書くのが通例である.
標本空間が実数 \(\mathbb{R}\) の場合, 確率空間 \((\mathbb{R}, \mathcal{A}, P)\) の完全加法族 \(\mathcal{A}\) はどうとるか.
確率空間の定義上, 標本空間のすべての部分集合に対して確率を与える必要はなかった. これは, 連続型確率分布を考える際に, 積分が定義できないような部分集合を避けるためである. 例えば, 標本空間が \(\mathbb{R}\) のとき, 完全加法族としては \(\mathbb{R}\) におけるボレル集合族 \(\mathcal{B}(\mathbb{R})\) をとるのが一般的である.
逆に条件 (D1) (D2) から出発してもよい.
つまり, 条件 (D1) (D2) を満たす関数 \(f(x)\) を単に確率密度関数と呼び, 実数 \(\mathbb{R}\) におけるボレル集合 \(B\) に対して, \(P(B) = \int_B f(x) dx\) と定めると, \((\mathbb{R}, \mathcal{B}(\mathbb{R}), P)\) は確率空間になる.
コメント