確率変数の基礎と離散型・連続型の考え方について解説します. この記事は初学者向けの直感的な解説を含みます. 数学的に厳密な取り扱い方や発展的な内容は次の記事を参照してください.
・確率変数と累積分布関数・確率質量関数・確率密度関数【上級編】
確率変数
確率変数とは, 取り得る値(または値の範囲)に確率が与えられている変数のこと
例. 2枚のコインを投げるとき, 表の出る枚数を \(X\) とすると, \(X\) の確率は表のようになる. このように, 取り得る値に確率が定まっている変数を確率変数という.
| \(X\) | 0 | 1 | 2 | 計 |
| 確率 | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(\frac{1}{4}\) | \(1\) |
- 確率変数は \(X, Y, \cdots\) などの大文字で表すことが多い. またその実現値は \(x,y ,a,b\) などの小文字で表すことが多い.
- \(X=a\) となる確率を \(P(X=a)\) と表す. また \(a\leq X \leq b\) となる確率を \(P(a\leq X \leq b)\) などと表す.
- 確率変数の取り得る値と確率との対応関係を確率分布といい, 確率変数はその確率分布に従うという.
離散型確率変数
確率変数には大きく分けて離散型と連続型がある. 離散型とは, 確率変数の実現値が, \(\{1, 2, 3, \cdots\}\) などのようにとびとびの値になっているもののことをいう.
(「とびとびの値」とはもう少し厳密にいうと「高々可算個の値」という意味である. )
確率変数 \(X\) がとびとびの値をとるとき, 離散型という.
上のコインの例は離散型である.
一般に, 離散型確率変数の取り得る値が \(x_1, x_2, \ldots \) であり, その確率が \(p_1, p_2, \ldots\) であるとき, 右のような表を確率分布表という.
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | 1 |
【代表的な離散型確率分布】
・二項分布
・ポアソン分布
・多項分布
・幾何分布
・超幾何分布
連続型確率変数
身長, 体重, 温度などのように連続的な値(実数のある範囲)をとるときは連続型といい, 離散型とは考え方が異なる.
確率変数 \(X\) は連続的な値をとるとき, 連続型という.
連続型のときは, 次のようにある曲線の下の面積(積分)で確率を考える.
任意の2つの実数 \(a, b\) (\(a<b\)) について, 確率変数 \(X\) が \(a\leq X \leq b\) となる確率 \(P(a\leq X \leq b)\) を\[
P(a\leq X \leq b)=\int_a^b f_X(x) dx
\]と積分表示できるとき, 関数 \(f_X(x)\) を \(X\) の確率密度関数という.
これは次のような直感に基づく.
例えば, 何人かの身長のデータを測定したときに, ヒストグラム全体の面積が1となるようにすれば, ある人の身長 \(X\) が区間 \([a,b]\) に入る確率 \(P(a\leq X\leq b)\) は, その区間上のヒストグラムの面積で近似できる. ヒストグラムは, サンプル数を大きくして, 階級の幅を狭めていくと, なめらかな曲線に近づくと考えられ, 確率 \(P(a\leq X\leq b)\) はその曲線で与えられる面積とみなすことができる.
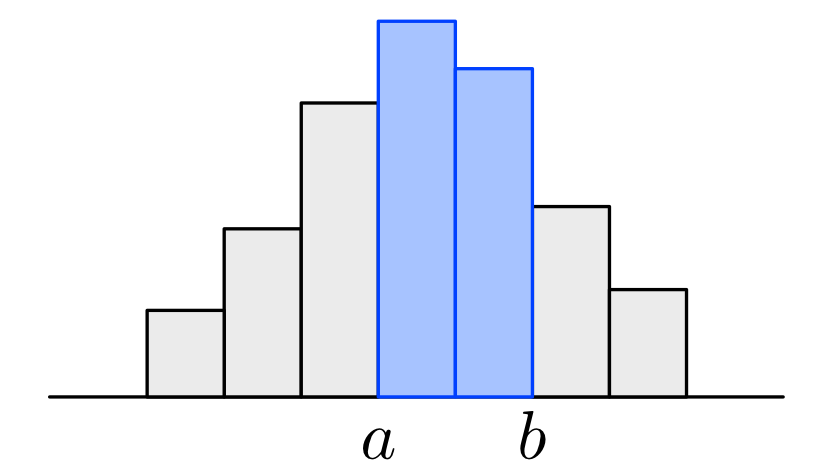
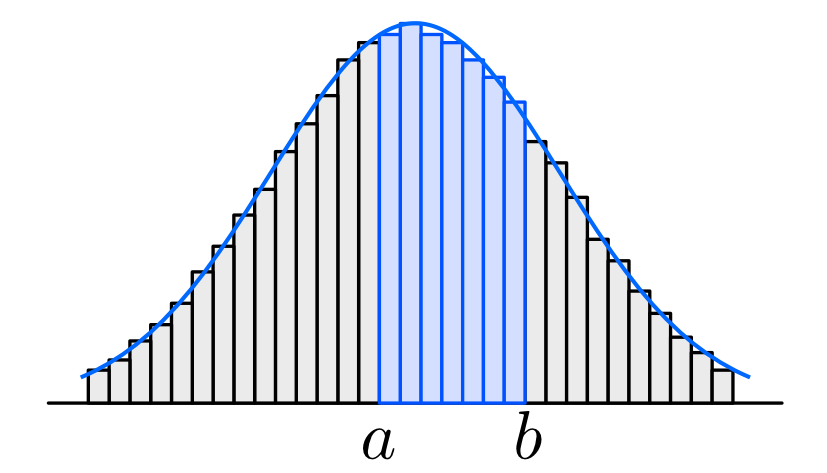
このアイディアを数学的に捉えたものが確率密度関数である.
注意. 連続型のときは, 確率変数 \(X\) がただ1つの値 \(a\) をとる確率は \(P(X=a)=0\) となる.
例えば身長の例でいえば, 測定器具の制度によっては身長が160cmと測定されることはありえても, 身長が一切の誤差なくちょうど160cmになることはほぼあり得ない. そのような確率は 0 と捉えるのが自然である.
確率密度関数 \(f_X(x)\) は次の性質をもつ.
(1) \(\displaystyle \int_{-\infty}^{\infty} f_X(x) dx =1\)
(2) 任意の実数 \(x\) に対して, \(f_X(x) \geq 0\) .
(1) は確率の総和は1であることから, (2) は確率は常に正であることから成り立つ.
(1)の証明には厳密には確率の連続性という性質を用いる必要がある.
詳細 → 確率変数と累積分布関数・確率質量関数・確率密度関数【上級編】
例題. 連続型確率変数 \(X\) の確率密度関数が, \[f_X(x)=\begin{cases}
k(x^2-1) & (-1\leq x \leq 1),\\ 0 & (x<-1, 1<x)
\end{cases}\]となっているとき, 定数 \(k\) の値を求めよ. また確率 \(P(0\leq x\leq \frac{1}{2})\) を求めよ.
解答. 確率の総和は \(1\) だから, \(\displaystyle \int_{-\infty}^{\infty} f_X(x) dx=1\). 左辺を計算すると\begin{align}\int_{-1}^{1} k(x^2-1) dx&= k \left[ \frac{1}{3}x^3 -x \right]_{-1}^1\\
&=-\frac{4}{3}k
\end{align}よって \(k=-\dfrac{3}{4}\). したがって, \begin{align}
P(0\leq x\leq \frac{1}{2})&=\int_{0}^{1/2} -\frac{3}{4} (x^2-1)dx \\
&=-\frac{11}{32}.\end{align}
【代表的な連続型確率分布】
・一様分布
・正規分布
・指数分布
・ガンマ分布
・ベータ分布

コメント